Tożsamości Fibonacciego w SymPy#
W tym prostym tutorialu zwerifikujemy szereg tożsamości spełnianych przez liczby Fibonacciego stosując bibliotekę SymPy. Zauważmy, że uda nam się kompletnie udowodnić tożsamości, które do tej pory nie było możliwe do weryfikacji bez ręcznych kroków w czystym SageMath.
from sympy import *
init_printing(use_unicode=True)
n=symbols('n',nonnegative=True,integer=True) #inicjalizujemy obiekty SymPy
phi=1/2*sqrt(5) + 1/2 #modelujemy liczby Fibonacciego korzystając z formuły Bineta
phihat=-1/2*sqrt(5) + 1/2
def FibBin(n):
return 1/sqrt(5)*(phi^n-phihat^n)
Ćw. 1: Dowód tożsamości Cassiniego#
\(F_n^2 - F_{n+1}F_{n-1}=(-1)^{n-1}\)
a=FibBin(n)^2-FibBin(n+1)*FibBin(n-1)-(-1)^(n-1)
a=expand(a) ## this is using expand and simplify from SymPy package
a=simplify(a)
a

Ćw. 2: Dowód tożsamości Catalana#
\(F_n^2-F_{n+r}F_{n-r}=(-1)^{n-r}F_{r}^2\)
r=symbols('r',nonnegative=True,integer=True)
a=((FibBin(n)^2-FibBin(n+r)*FibBin(n-r)))/((-1)^(n-r)*(FibBin(r)^2))
a=powsimp(a)
a=simplify(a)
a=radsimp(a)
a=expand(a)
a=factor(a)
a=powsimp(a)
a=radsimp(a)
a=expand(a)
simplify(a-1)

Ćw. 3: Dowód tożsamości Ocagne’a#
\(F_{r} F_{n+1}-F_{r+1}F_{n}=(-1)^n F_{r-n}\)
a=(FibBin(r)*FibBin(n+1)-FibBin(r+1)*FibBin(n))/((-1)^n*FibBin(r-n))
a=simplify(a)
a-1

Ćw.4: Dowód następującej tożsamości#
\(\sum_{i=1}^{n}F_{i}=F_{n+2}-1\)
i=var('i')
a=Sum(FibBin(i),(i,1,n))#Sum is a command from SymPy
a=a.doit() #one needs to force SymPy to evaluate the sum
a=a-(FibBin(n+2)-1)
a=simplify(a)
a
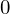
Ćw.5: Dowód następującej tożsamości#
\(\sum_{i=1}^{n} F_i^2 = F_n \cdot F_{n+1}\)
s1=Sum(FibBin(i)^2,(i,1,n))
s2=(FibBin(n)*FibBin(n+1))
s1=s1.doit()
simplify(s1-s2)
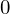
Wyzwanie: Dowód tożsamości eliptycznej Warda (Ward’s elliptic divisibility identity)#
\(F_{4n+2}F_2^3-F_{2n+4}F_{2n}^3+F_{2n+2}^3 F_{2n-2}=0\) for all \(n\geq 0\).
a=FibBin(4*n+2)*FibBin(2)^3-FibBin(2*n+4)*FibBin(2*n)^3+FibBin(2*n+2)^3*FibBin(2*n-2)
a=a.radsimp()
a=a.simplify()
a=a.expand()
a=a.simplify()
a=a.simplify()
a

