Zadania domowe, zestaw 1#
W tym zestawie zadań proszę przygotować kod, który będzie generował rozwiązania zadań podanych w tekście.
Zadanie 1#
Zaprojektuj kod, który iteracyjnie obliczy kolejny wyraz rekurencji
\[F_{n+2}=AF_{n+1}+BF_{n},\]
\[F_0=a_0,\quad F_1=a_1\]
# rownanie
def Rek(a0,a1,A,B):
xn=a0
xn1=a1
n=0
while True: #wisząca pętla
xn1,xn=A*xn1+B*xn,xn1
n+=1
print(n)
yield xn1 #leniwa ewaluacja
Fib=Rek(0,1,1,-1)
Primes()[5]
13
[next(Fib) for _ in range(0,10)]
11
12
13
14
15
16
17
18
19
20
[0, 1, 1, 0, -1, -1, 0, 1, 1, 0]
#x=var('x')
#((x-1)**2).expand()
a,b=var('a,b')
R=Rek(a,b,2,-1)
[next(R).expand() for _ in range(0,10)]
[-a + 2*b,
-2*a + 3*b,
-3*a + 4*b,
-4*a + 5*b,
-5*a + 6*b,
-6*a + 7*b,
-7*a + 8*b,
-8*a + 9*b,
-9*a + 10*b,
-10*a + 11*b]
#x=var('x')
#((x-2)**2).expand()
a,b=var('a,b')
R=Rek(a,b,4,-4)
[next(R) for _ in range(0,10)]
[-4*a + 4*b,
-16*a + 12*b,
-48*a + 32*b,
-128*a + 80*b,
-320*a + 192*b,
-768*a + 448*b,
-1792*a + 1024*b,
-4096*a + 2304*b,
-9216*a + 5120*b,
-20480*a + 11264*b]
# generator
def ResztyModN(a,N):
a0=0
while True:
if (a0%N == a):
yield a0
a0+=1
gen=ResztyModN(17,57)
[next(gen) for _ in range(0,10)]
[17, 74, 131, 188, 245, 302, 359, 416, 473, 530]
Zadanie 2#
Dany jest wielomian \(x^2+m\cdot x+1\), którego pierwiastkami są \(\alpha,\beta\). Wyznacz postać wyrażenia
\[\frac{1}{\alpha^3}+\frac{1}{\beta^3}\]
jako funkcji zmiennej \(m\).
x=var('x')
m=var('m')
a,b=var('a,b')
expr=(x^2+m*x+1)-(x-a)*(x-b)
expr.collect(x)
-a*b + (a + b + m)*x + 1
expr.coefficients(x,sparse=False)
[-a*b + 1, a + b + m]
c=var('c')
assume(c==1)
bool(c^2==1)
True
forget(c==1)
(1/a^3+1/b^3).factor()
(a^2 - a*b + b^2)*(a + b)/(a^3*b^3)
ee=((1/a^3+1/b^3).factor())
ee.subs({b:-a-m}).factor()
(3*a^2 + 3*a*m + m^2)*m/((a + m)^3*a^3)
(-a*b+1).subs({b:-a-m}).factor()
a^2 + a*m + 1
(ee.subs({b:-a-m}).factor()).subs({a^2:-a*m-1})
(m^2 - 3)*m/((a + m)^3*a^3)
(ee.subs({b:-a-m}).factor()).subs({a^2:-a*m-1})
(m^2 - 3)*m/((a + m)^3*a^3)
#a^3==a*(-a*m-1)
(a*(-a*m-1)).expand()
-a^2*m - a
(-(-a*m-1)*m - a).expand()
a*m^2 - a + m
((a + m)^3).expand()
a^3 + 3*a^2*m + 3*a*m^2 + m^3
(((a + m)^3).expand()).subs({a^3:a*m^2 - a + m})
3*a^2*m + 4*a*m^2 + m^3 - a + m
(((a + m)^3).expand()).subs({a^3:a*m^2 - a + m}).subs({a^2:-a*m-1}).expand()
a*m^2 + m^3 - a - 2*m
((a*m^2 + m^3 - a - 2*m)*(a*m^2 - a + m)).expand()
a^2*m^4 + a*m^5 - 2*a^2*m^2 - 2*a*m^3 + m^4 + a^2 + a*m - 2*m^2
((a*m^2 + m^3 - a - 2*m)*(a*m^2 - a + m)).expand().collect(a)
m^4 + (m^4 - 2*m^2 + 1)*a^2 + (m^5 - 2*m^3 + m)*a - 2*m^2
((a*m^2 + m^3 - a - 2*m)*(a*m^2 - a + m)).expand().collect(a).subs({a^2:-a*m-1}).expand()
-1
#zatem
#(m^2 - 3)*m/((a + m)^3*a^3)
#upraszcza sie do
((m^2 - 3)*m/(-1)).expand()
-m^3 + 3*m
Odpowiedź:
Dany jest wielomian \(x^2+m\cdot x+1\), którego pierwiastkami są \(\alpha,\beta\). Mamy
\[\frac{1}{\alpha^3}+\frac{1}{\beta^3}=-m^3+3m.\]
#weryfikacja numeryczna
m1=3
sol=solve(x^2+m1*x+1,x)
roo=[s.rhs() for s in sol]
bool((1/roo[0]^3+1/roo[1]^3).simplify_full()==-m1^3+3*m1)
True
#rozwiązanie błyskawiczne z użyciem pierścienia ilorazowego
R.<aa,bb,mm>=PolynomialRing(Rationals(),3)
I=R.ideal([aa*bb-1,aa+bb+mm]) #relacje
S.<abar,bbar,mbar>=R.quotient_ring(I)
1/abar^3+1/bbar^3
-mbar^3 + 3*mbar
Zadanie 3#
W momencie początkowym jesteśmy w punkcie (0,0) na płaszczyźnie i patrzymy na północ. W kroku parzystym obracamy się w lewo i idziemy krok do przodu, w kroku nieparzystym obracamy się w prawo, robimy dwa kroki do przodu i obracamy się w lewo.
Udowodnij, że spacer powtarza się co 9 kroków.
def Spacer():
pos = 0
kier = i #==sqrt(-1)
while True:
kier *= i^3
pos += 2*kier
kier *= i
yield pos
kier *= i
pos += kier
yield pos
s=Spacer()
a=0*i
b=next(s)
gra=arrow(a,b)
for _ in range(0,20):
a,b=b,next(s)
gra += arrow(a,b)
gra
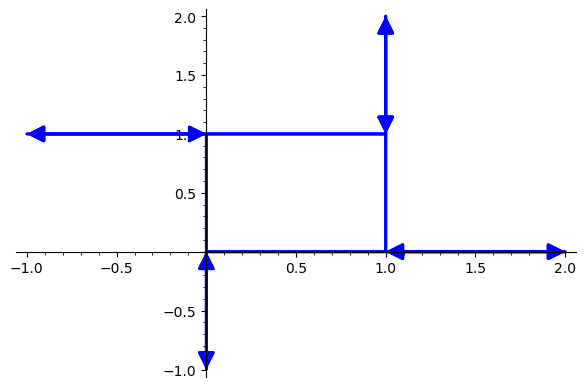
s=Spacer()
[next(s) for _ in range(0,10)]
[2, 1, 2*I + 1, I + 1, I - 1, I, -I, 0, 2, 1]
Zadanie 4#
Liczba \(m\) jest równa odwrotności powiększonej o \(1\) liczby \(m\). Wyznacz \(m^{10}\).
m=var('m')
[(m^10).subs({m:x.rhs()}).expand() for x in solve(m-1/(1+m),m)]
[55/2*sqrt(5) + 123/2, -55/2*sqrt(5) + 123/2]
#rozwiązanie z pierścieniem ilorazowym
R2.<T>=PolynomialRing(Rationals())
polrel=(T-(1/(1+T))).numerator()
Q2.<m>=R2.quotient_ring(R2.ideal(polrel))
m^10
-55*m + 34
Zadanie 5#
Niech \(G=\{(a,b)\in \mathbb{C}^2: a^2+b^2\neq 0\}\). Na zbiorze \(G\) wprowadzamy operację:
\[m:G\times G\rightarrow G\]
\[m((a,b),(u,v))=(au-bv,av+bu)\]
Uzasadnij, że \((G,m)\) jest grupą abelową. Wyznacz wszystkie elementy rzędu \(4\) i \(6\) w tej grupie.
class gr:
def __init__(self,a,b):
self.x=a
self.y=b
def __mul__(self,ob):
a=self.x
b=self.y
u=ob.x
v=ob.y
x1=a*u-b*v
y1=b*u+a*v
return gr(x1,y1)
def __inv__(self):
a=self.x
b=self.y
return gr(a/(a^2+b^2),-b/(a^2+b^2))
def __eq__(self,ob):
if (self.x==ob.x) and (self.y==ob.y):
return True
else:
return False
def __repr__(self):
return "("+str(self.x)+","+str(self.y)+")"
def coords(self):
return [self.x,self.y]
#działanie jest zamknięte (uzasadnij, że jesli (a,b), (u,v) należą do G, to (au-bv,av+bu) nalezy do G, tzn. )
a,b,u,v=var('a,b,u,v')
print(gr(a,b)*gr(u,v))
eqs=[a*u==b*v,b*u==-a*v]
solv=solve(eqs,(a,b,u,v))
#wszystkie rozwiazania spełniają albo a^2+b^2=0, albo u^2+v^2=0
[[(a^2+b^2).subs(s),(u^2+v^2).subs(s)] for s in solv]
(a*u - b*v,b*u + a*v)
[[r41^2 + r42^2, 0], [0, 0], [0, 0], [0, r47^2 + r48^2]]
#łączność
a,b=var('a,b')
c,d=var('c,d')
e,f=var('e,f')
ll=(gr(a,b)*gr(c,d))*gr(e,f)
rr=gr(a,b)*(gr(c,d)*gr(e,f))
assert (ll.x-rr.x).expand() == 0
assert (ll.y-rr.y).expand() == 0
#el. neutralny
a,b=var('a,b')
el1=(gr(1,0)*gr(a,b))
el2=(gr(a,b)*gr(1,0))
assert bool(el1==el2) #these tuples are not identical as Python objects unless we define properly the __eq__ method
assert bool(el1==gr(a,b))
#odwrotnosc
a,b=var('a,b')
assert (gr(a,b)*gr(a/(a^2+b^2),-b/(a^2+b^2))).x.simplify_full()==1
assert (gr(a,b)*gr(a/(a^2+b^2),-b/(a^2+b^2))).y.simplify_full()==0
#inna metoda
assert bool(gr(a,b)*gr(a/(a^2+b^2),-b/(a^2+b^2))==gr(1,0))
assert bool(gr(a/(a^2+b^2),-b/(a^2+b^2))*gr(a,b)==gr(1,0))
#elementy rzedu 4
a,b=var('a,b')
g=gr(a,b)
ginv=gr(a,b).__inv__() #element odwrotny; nie mamy jeszcze implementacji potęgowania więc napisanie gr(a,b)^(-1) lub gr(a,b)**(-1) nie zadziała
v=vector((g*g).coords())-vector((g*g).__inv__().coords()) #odjęcie list jako wektorów (wygodny trik)
eqs=[v[0].factor().numerator(),v[1].factor().numerator()] #równania definiujące elementy rzędu 1,2 lub 4
solv=solve(eqs,(a,b))
els=[gr(a.subs(s),b.subs(s)) for s in solv] #elementy rzędów 1, 2 lub 4; które mają rząd 4?
def Order(g,bound):
n=0
e=gr(SR(1),SR(0))
el=e #pierścień symboliczny SR (uwaga, w przypadku grup na innych pierścieniach trzeba to zmodyfikować)
while n<bound:
n+=1
el*=g
if el == e:
return n
print("Rząd elementu nie został określony")
print(g)
return 0
[g for g in els if Order(g,100) == 4]
Rząd elementu nie został określony
(0,0)
[(-I,0),
(I,0),
(0,-1),
(0,1),
(-1/2*I - 1/2,-1/2*I - 1/2),
(1/2*I - 1/2,1/2*I - 1/2),
(-1/2*I + 1/2,-1/2*I + 1/2),
(1/2*I + 1/2,1/2*I + 1/2),
(-1/2*I - 1/2,1/2*I + 1/2),
(1/2*I - 1/2,-1/2*I + 1/2),
(-1/2*I + 1/2,1/2*I - 1/2),
(1/2*I + 1/2,-1/2*I - 1/2)]
v2=vector((g*g*g).coords())-vector((g*g*g).__inv__().coords()) #odjęcie list jako wektorów (wygodny trik)
eqs2=[v2[0].factor().numerator(),v2[1].factor().numerator()] #równania definiujące elementy rzędu 1,2 lub 4
solv2=solve(eqs2,(a,b))
els2=[gr(a.subs(s),b.subs(s)) for s in solv2] #elementy rzędów 1, 2, 3 lub 6; które mają rząd 6?
[g for g in els2 if Order(g,100) == 6]
Rząd elementu nie został określony
(0,0)
[(-1/2*I*sqrt(3) + 1/2,0),
(1/2*I*sqrt(3) + 1/2,0),
(0,-1/2*sqrt(3) - 1/2*I),
(0,1/2*sqrt(3) + 1/2*I),
(0,-1/2*sqrt(3) + 1/2*I),
(0,1/2*sqrt(3) - 1/2*I),
(-1/4*I*sqrt(3) - 3/4,-1/4*sqrt(3) - 1/4*I),
(-1/4*I*sqrt(3) - 3/4,1/4*sqrt(3) + 1/4*I),
(1/4*I*sqrt(3) - 3/4,-1/4*sqrt(3) + 1/4*I),
(1/4*I*sqrt(3) - 3/4,1/4*sqrt(3) - 1/4*I),
(-1/4*I*sqrt(3) + 3/4,-1/4*sqrt(3) + 1/4*I),
(-1/4*I*sqrt(3) + 3/4,1/4*sqrt(3) - 1/4*I),
(1/4*I*sqrt(3) + 3/4,-1/4*sqrt(3) - 1/4*I),
(1/4*I*sqrt(3) + 3/4,1/4*sqrt(3) + 1/4*I),
(1/2,-1/2*sqrt(3)),
(1/2,1/2*sqrt(3)),
(-1/4*I*sqrt(3) - 1/4,-1/4*sqrt(3) - 3/4*I),
(-1/4*I*sqrt(3) - 1/4,1/4*sqrt(3) + 3/4*I),
(1/4*I*sqrt(3) - 1/4,-1/4*sqrt(3) + 3/4*I),
(1/4*I*sqrt(3) - 1/4,1/4*sqrt(3) - 3/4*I),
(-1/2*I*sqrt(3),-1/2*I),
(-1/2*I*sqrt(3),1/2*I),
(1/2*I*sqrt(3),-1/2*I),
(1/2*I*sqrt(3),1/2*I)]