Ctrl+K

Bazy Groebnera: teoria i zastosowania

Bazy Groebnera: teoria i zastosowania#

W niniejszym pliku prześledzimy zastosowania baz Groebnera do rozwiązywania problemów o naturze geometrycznej. Podstawowym pojęciem będzie pierścień wielomianów pewnej liczby zmiennych. Będziemy operowali ideałami w tym pierścieniu i zobaczymy jak operacje na ideałach pozwalają nam dowodzić stwierdzeń geometrycznych o pewnych obiektach zdefiniowanych algebraicznie.

Baza Groebnera \(B\) dla ideału \(I\) w \(R=K[x_1,\ldots x_n]\) to baza tego ideału, która spełnia warunek, że dzielenie z resztą dowolnego wielomianu z \(R\) przez element z bazy \(B\) daje jednoznacznie określoną resztę.

Przykład 1#

Oblicz bazę Groebnera dla ideału \(I=\langle x^2+y^2-1,x+y \rangle \subset \mathbb{Q}[x,y]\). Uwaga, baza Groebnera zależy od przyjętego porządku na jednomianach.

R.<x,y>=PolynomialRing(Rationals(),2)
I=R.ideal([x^2+y^2-1,x+y])
I.groebner_basis()

[y^2 - 1/2, x + y]

R.<y,x>=PolynomialRing(Rationals(),2)
I=R.ideal([x^2+y^2-1,x+y])
I.groebner_basis()

[x^2 - 1/2, y + x]

Dzielenie z resztą wielomianów przez elementy z bazy Groebnera pozwala jednoznacznie je zredukować.

aa=(x^3+y^3-1)
bb=(x^2+y^2-1)
cc=(x+y)

aa-y^2*cc-x^2*cc

-y^2*x - y*x^2 - 1

dd=y^2-1/2

aa-y^2*cc-x^2*cc+dd*x+y*x*cc-dd*x

-1

aa+1 in I

True

Niech \(V(S) = \{(x_1,\ldots,x_n)\in K^n: \forall_{f\in S} f(x_1,\ldots,x_n)=0\}\) będzie zbiorem zer podzbioru wielomianów \(S\). Jest to inaczej zbiór rozwiązań układu równań algebraicznych zadanych przez bazę ideału rozpiętego na elementach \(S\).

Obliczanie bazy Grobnera \(B(I)\) ideału \(I\) pozwala uprościć opis zbioru \(V(I)\).

Ponadto \(V(I) = V(B(I))\)

Przykład 2#

Wyznacz zbiór \(V(I)\) zer w \(\mathbb{Q}\) układu równań \(x^3+y^3-1=0\), \(x+y-1=0\) (inaczej ideału \(I=\langle x^3+y^3-1, x+y-1 \rangle\))

R.<x,y>=PolynomialRing(Rationals(),2)
I=R.ideal([x^3+y^3-1,x+y-1])
I.groebner_basis()

[y^2 - y, x + y - 1]

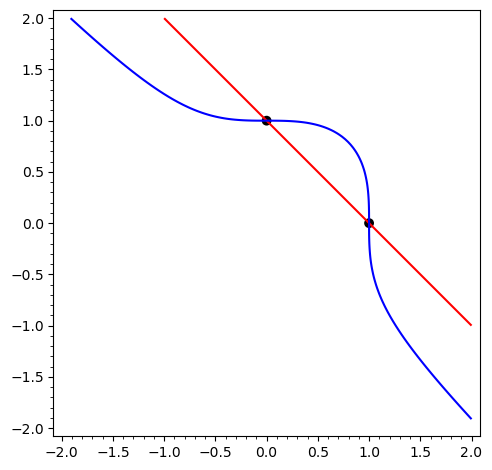
Zatem \(V(I)\) jest równoważnie zbiorem rozwiązań układu \(y^2-y=0\), \(x+y-1\). Pierwsze równanie ma rozwiązania w \(\mathbb{Q}\) postaci \(y=0,1\). Odpowiadające im wartości zmiennej \(x\) to \(x=1\) i \(x=0\), odpowiednio.

V=AffineSpace(R).subscheme(I)
V.rational_points()

[(0, 1), (1, 0)]

X,Y=var('X,Y')

gra=Graphics()
gra+=implicit_plot(X+Y-1,(X,-2,2),(Y,-2,2),color='red')
gra+=point((0,1),pointsize=50,color='black')+point((1,0),pointsize=50,color='black')
gra+=(implicit_plot(X^3+Y^3-1,(X,-2,2),(Y,-2,2)))

gra.show()
_images/2567783a1dacb016af8d637ee3396106b182a8a6763bee1c9707c00348794589.png

Przykład 3#

Wyznacz ekstrema funkcji \(f(x,y)=x+y^2\) na elipsie \(x^2+2y^2=3\).

Stosujemy do tego zadania technikę mnożników Lagrange’a.

Niech \(F(x,y,m)=f(x,y)-m (x^2+2 y^2-3)\). Obliczamy ideał \(I\) w \(K[x,y,m]\) zadany pochodnymi cząstkowymi \(\delta_{x}F(x,y,m),\delta_{y}F(x,y,m),\delta_{m}F(x,y,m)\).

Wyznaczamy zbiór \(V(I)\) (stosując najlepiej bazę Groebnera).

R.<x,y,m>=PolynomialRing(Rationals(),3)
F=x+y^2-m*(x^2+2*y^2-3)

I=R.ideal([F.derivative(t) for t in [x,y,m]])
I.groebner_basis()

[x^2 - x + 6*m - 3, x*y - y, y^2 + 1/2*x - 3*m, x*m - 1/2, y*m - 1/2*y, m^2 + 1/12*x - 1/2*m - 1/12]

Baza Groebnera poprzez wygodne faktoryzacje wielomianów pozwala nam rozłożyć zbiór \(V(I)\) na sumę innych algebraicznych zbiorów.

AffineSpace(R).subscheme(I.groebner_basis()).irreducible_components()

[
Closed subscheme of Affine Space of dimension 3 over Rational Field defined by:
  2*m - 1,
  y - 1,
  x - 1,
Closed subscheme of Affine Space of dimension 3 over Rational Field defined by:
  2*m - 1,
  y + 1,
  x - 1,
Closed subscheme of Affine Space of dimension 3 over Rational Field defined by:
  y,
  x - 6*m,
  12*m^2 - 1
]

Zatem ekstrema funkcji \(f(x,y)\) na elipsie \(x^2+y^2-3=0\) zawierają się w zbiorze:

\((x,y)=(1,1)\), \((x,y)=(1,-1)\) oraz \((x,y)=(\pm\sqrt{3},0)\).

(x+y^2).subs({x:1,y:1})

2

(x+y^2).subs({x:1,y:-1})

2

(x+y^2).subs({x:sqrt(3),y:0})

sqrt(3)

(x+y^2).subs({x:-sqrt(3),y:0})

-sqrt(3)

Zatem maksimum dla funkcji \(f\) ograniczonej do elipsy pojawia się w punkcie \((1,1)\) i \((1,-1)\) i wynosi \(2\). Minimum pojawia się w puncie \((-\sqrt{3},0)\) i wynosi \(-\sqrt{3}\).

Wyznaczmy teraz ekstrema obliczając parametryzację elipsy i podstawiając \(x=x(t)\) oraz \(y=y(t)\) do funkcji \(f(x,y)\) i obliczając ekstremum funkcji \(g(t)=f(x(t),y(t))\).

Parametryzacja elipsy#

Znajdujemy jeden punkt na elipsie, np. \((1,1)\).

Wyznaczamy pęk prostych przechodzących przez zadany punkt, np.

\(L:t x+ b = y\)

\(L\) zawiera punkt \((1,1)\), zatem \(t+b = 1\), stąd \(L: t x + (1-t) = y\).

Podstawiamy zmienną \(y\) do równania elipsy i wyznaczamy zmienną \(x\) jako funkcję \(t\).

R.<x,y,t>=PolynomialRing(Rationals(),3)
f2=(x^2+2*y^2-3).subs({y:t*x+(1-t)}).factor()[1][0]

X,T=var('X,T')
eq1=f2.subs({x:X,t:T})
xt=solve(eq1,X)[0].rhs().subs({T:t})
yt=t*xt+(1-t)
(x^2+2*y^2-3).subs({x:xt,y:yt}).subs({t:T}).simplify_full()

0

gt=(x+y^2).subs({x:xt,y:yt}).subs({t:T}).simplify_full()

gt

8*(T^4 - T)/(4*T^4 + 4*T^2 + 1)

gt.derivative(T).simplify_full().factor()

8*(2*T^2 + 2*T - 1)*(2*T + 1)/(2*T^2 + 1)^3

sol=solve((2*T^2 + 2*T - 1)*(2*T + 1),T)
sol

[T == -1/2*sqrt(3) - 1/2, T == 1/2*sqrt(3) - 1/2, T == (-1/2)]

plot(gt,(t,-20,20))
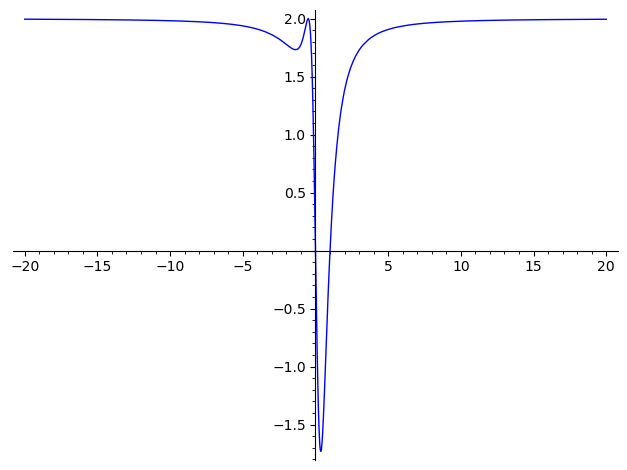
_images/15d0b3a5db205f8976d7bf6d2b368b86e9b96634edff3aa65dc544c8b42f9967.png 
plot(gt.derivative(T),(T,-10,10))
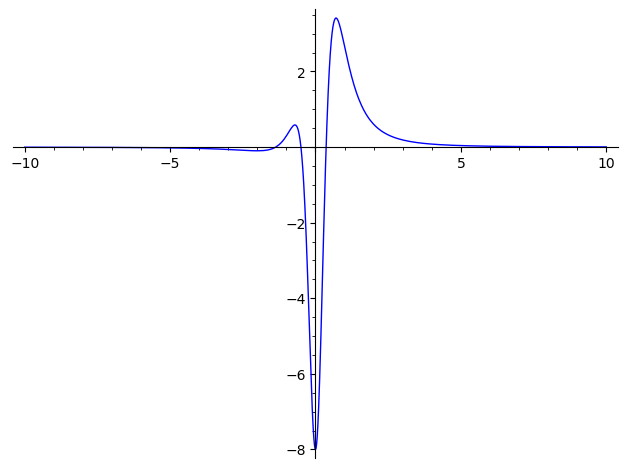
_images/111d004ae16dc039316b4b38a0bc96869107fa12d4a2f922bfa254ee19284e1f.png 
xt.subs({t:-1/2})

1

Z.<x>=PolynomialRing(Rationals())
pol=2*x^2 + 2*x - 1
K.<t1>=NumberField(pol)

xv=(2*t1^2 - 4*t1 - 1)/(2*t1^2 + 1) #xt
yv=(2*t1^2 - 4*t1 - 1)*t1/(2*t1^2 + 1) - t1 + 1 #yt

(xv,yv)

(-2*t1 - 1, 0)

xv.minpoly()

x^2 - 3

Przykład 4#

Kolorowanie grafu. Ile jest różnych kolorowań cyklu 4 elementowego n kolorami?

R=PolynomialRing(Rationals(),4,'x')
R.gens()

(x0, x1, x2, x3)

#wielomian wierzchołkowy

N=3 #liczba kolorów

gens=R.gens()
F=lambda x: prod([x-i for i in range(0,N)])

vpol=[F(x) for x in gens] #wielomiany wierzchołkowe

n=len(gens)
epol=[(F(gens[i])-F(gens[(i+1)%n]))/(gens[i]-gens[(i+1)%n]) for i in range(0,n)]  #wielomiany krawędziowe

Teraz wykorzystamy bazy Groebnera do obliczenia liczby rozwiązań.

V=AffineSpace(R).subscheme(R.ideal(vpol + epol).groebner_basis())

V.rational_points()

[(0, 1, 0, 1),
 (0, 1, 0, 2),
 (0, 1, 2, 1),
 (0, 2, 0, 1),
 (0, 2, 0, 2),
 (0, 2, 1, 2),
 (1, 0, 1, 0),
 (1, 0, 1, 2),
 (1, 0, 2, 0),
 (1, 2, 0, 2),
 (1, 2, 1, 0),
 (1, 2, 1, 2),
 (2, 0, 1, 0),
 (2, 0, 2, 0),
 (2, 0, 2, 1),
 (2, 1, 0, 1),
 (2, 1, 2, 0),
 (2, 1, 2, 1)]

len(V.rational_points()) #liczba kolorowań trzema kolorami

18

#liczba kolorowań N kolorami cyklu długosci m

def Kol(N,m):
    R=PolynomialRing(Rationals(),m,'x')
    gens=R.gens()
    F=lambda x: prod([x-i for i in range(0,N)])
    vpol=[F(x) for x in gens] #wielomiany wierzchołkowe
    n=len(gens)
    epol=[(F(gens[i])-F(gens[(i+1)%n]))/(gens[i]-gens[(i+1)%n]) for i in range(0,n)]  #wielomiany krawędziowe
    V=AffineSpace(R).subscheme(R.ideal(vpol + epol).groebner_basis())
    return V.rational_points()

[len(Kol(2,i)) for i in range(2,10)]

[2, 0, 2, 0, 2, 0, 2, 0]

[len(Kol(3,i)) for i in range(2,10)]

[6, 6, 18, 30, 66, 126, 258, 510]

[len(Kol(4,i)) for i in range(2,7)]

[12, 24, 84, 240, 732]

len(Kol(3,5).rational_points())

30

Przykład 5#

Niech \(a,b,c\) będą pewnymi liczbami zespolonymi. Wiedząc, że

\(a+b+c=m,\)

\(a^2+b^2+c^2=n,\)

\(a^3+b^3+c^3=k\)

wyznacz sumę \(a^4+b^4+c^4\) jako wyrażenie zależne tylko od \(m,n,k\).

R.<a,b,c,m,n,k,r>=PolynomialRing(Rationals(),7)
eq1=[a+b+c-m,a^2+b^2+c^2-n,a^3+b^3+c^3-k,a^4+b^4+c^4-r]
I=R.ideal(eq1)
I.groebner_basis()

I.groebner_basis()

[m^4 - 6*m^2*n + 3*n^2 + 8*m*k - 6*r, c^3 - c^2*m + 1/2*c*m^2 - 1/6*m^3 - 1/2*c*n + 1/2*m*n - 1/3*k, b^2 + b*c + c^2 - b*m - c*m + 1/2*m^2 - 1/2*n, a + b + c - m]

relacja=I.groebner_basis()[0]

relacja

m^4 - 6*m^2*n + 3*n^2 + 8*m*k - 6*r

rozw=(8*k*m + m^4 - 6*m^2*n + 3*n^2)/6

relacja.subs({r:rozw})

0
Contents