Krzywa Hilberta#
Wypełniająca kwadrat krzywa Hilberta \(H:[0,1]\rightarrow [0,1]^2\) jest przykładem ciągłego odwzorowania, które pozwala przekształcić dwuwymiarowy obiekt na jednowymiarową reprezentację.
Wykorzystamy system Lindenmayera oparty na symbolach \(A,B,F\), \(+,-\) do reprezentacji skończonej rodziny krzywych \(H_{n}:[0,1]\rightarrow [0,1]^2\), które w granicy \(\lim_{n}H_n\) przybliżają krzywą Hilberta (pytanie: w jakim sensie jest opisana ta granica?)
System Lindenmayera dla krzywej \(H_n\):
alfabet: \(A,B\)
stałe: \(F,+,-\)
aksjomat \(A\)
reguły (re)produkcji: \(A\rightarrow +BF-AFA-FB+\), \(B\rightarrow -AF+BFB+FA-\)
Reguła \(F\) oznacza rysowanie jednostki, \(+\) oznacza skręt w lewo o \(90\) stopni, \(-\) oznacza skręt w prawo o \(90\) stopni. Symbole \(A\) i \(B\) są ignorowane podczas rysowania.
def F(state,gra): #narysuj linię w kierunku wynaczonym zmienną angle, z punktu (x,y) i o długości l
pos=state[0]
angle=state[1]
l=state[2]
x=pos[0]
y=pos[1]
xend=x+l*cos(angle)
yend=y+l*sin(angle)
draw=line([(x,y),(xend,yend)],axes=False,aspect_ratio=1)
gra=gra+draw
return [[xend,yend],angle,l],gra
def a(state,gra,delta): #obróć się o kąt delta
pos=state[0]
angle=state[1]
l=state[2]
x=pos[0]
y=pos[1]
return [[x,y],angle+delta,l],gra
def ApplyRule(str1,replrule): #zastosowanie reguł ze słownika replrule
return''.join([replrule[x] for x in str1])
#Trójkąt Sierpinskiego
def DrawHilb(str1,state,gra,angle):
while len(str1) >0:
s=str1[0]
schop=str1[1:len(str1)]
if s=="F":
state,gra=F(state,gra)
if s=="+":
state,gra=a(state,gra,angle)
if s=="-":
state,gra=a(state,gra,-angle)
str1=schop
return state,gra
axiomHilb="A"
replruleHilb={"A":"+BF-AFA-FB+","B":"-AF+BFB+FA-","+":"+","-":"-","F":"F"}
state0=[[0,0],0,1]
gra0=Graphics()
def f(s,n):
while n>0:
s,n=ApplyRule(s,replruleHilb),n-1
return s
for i in range(1,7):
_,qq=DrawHilb(f(axiomHilb,i),state0,gra0,pi/2)
show(qq,axes=False,aspect_ratio=1,figsize=[3,3])






Prześledzmy teraz sposób kodowania punktów z odcinka \([0,1]\) w kwadracie \([0,1]^2\) za pomocą krzywej \(H_n\). Odwołamy się do kodującego daną krzywą słowa z systemu Lindenmayera.
Startując z punktu \((0,0)\) w kierunku \([1,0]\) (kąt \(0\) stopni względem osi \(OX\)) zanalizujemy trajektorię ruchu pisaka, który modeluje krzywą \(H_1\).
f(axiomHilb,1)
'+BF-AFA-FB+'
Zgodnie z opisem słowa kodującego (ignorując symbole \(A,B\)) otrzymujemy następujący ciąg instrukcji:
(+) Obracamy wektor wodzący o \(90\) stopni przeciwnie do ruchu wskazówek zegara, wskazuje on kierunek \(k=[0,1]\).
(F) Poruszamy się o jednostkę w kierunku \(k\).
(-) Obracamy wektor wodzący o \(90\) stopni zgodnie z ruchem wskazówek zegara, wskazuje on kierunek \(k=[1,0]\).
(F) Poruszamy się o jednostkę w kierunku \(k\).
(-) Obracamy wektor wodzący o \(90\) stopni zgodnie z ruchem wskazówek zegara, wskazuje on kierunek \(k=[0,1]\).
(F) Poruszamy się o jednostkę w kierunku \(k\).
(+) Obracamy wektor wodzący o \(90\) stopni przeciwnie do ruchu wskazówek zegara, wskazuje on kierunek \(k=[1,0]\).
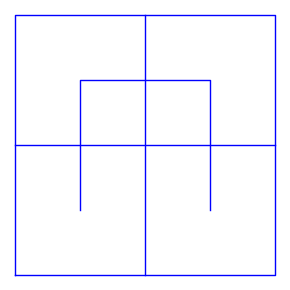
Przesuwając punkt startowy do \((1/4,1/4)\) oraz skalując jednostkę kroku (dla \(n=1\)) do \(1/2\) otrzymamy następującą krzywą \(H_1\).
def H1(t):
p0=vector([1/4,1/4])
if t<=1/3:
p=p0+(3*t)*vector([0,1/2])
return tuple(p)
if t<=2/3:
p=p0+vector([0,1/2])+(3*(t-1/3))*vector([1/2,0])
return tuple(p)
if t>2/3:
p=p0+vector([1/2,1/2])+(3*(t-2/3))*vector([0,-1/2])
return tuple(p)
print(t)
print("Poza skalą")
assert False
show(line([H1(0),H1(1/3),H1(2/3),H1(1)])+line([(0,0),(1,0),(1,1),(0,1),(0,0)])+line([(1/2,0),(1/2,1)])+line([(0,1/2),(1,1/2)]),aspect_ratio=1,figsize=[3,3],axes=False)
s=f(axiomHilb,2)
s1=s.replace('A','').replace('B','').replace('+-','').replace('-+','')
s1
'F+F+F-FF-F-F+F+F-F-FF-F+F+F'
#współrzędne odwiedzanych pikseli
def HVertices(n):
s=f(axiomHilb,n)
s1=s.replace('A','').replace('B','').replace('+-','').replace('-+','')
N=s1.count('F')
p=vector([0,0])
k=vector([1,0])
m=matrix(2,2,[0,-1,1,0])
mi=matrix(2,2,[0,1,-1,0])
piks=[tuple(p)]
for el in s1:
if el=='F':
p=p+k
piks.append(tuple(p))
if el=='+':
k=m*k
if el=='-':
k=mi*k
return piks
show(line(HVertices(2)),axes=False,aspect_ratio=1)

show(line(HVertices(3)),axes=False,aspect_ratio=1)
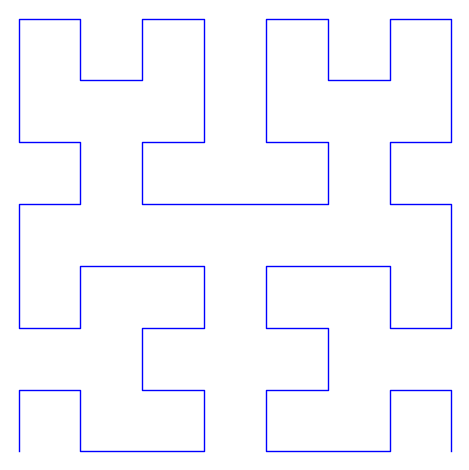
H4=HVertices(4)
#ignorowanie komunikatów technicznych
import warnings
warnings.filterwarnings("ignore")
matrix_plot(matrix(16,16,[(i-4*j)%4/4 for i in range(0,16) for j in range(0,16)]))
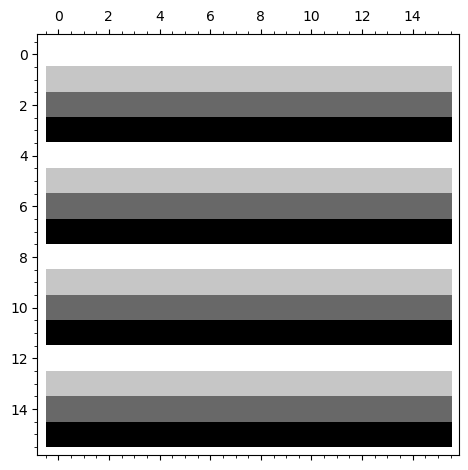
m=matrix(16,16,[(i+4*j)%4/4 for i in range(0,16) for j in range(0,16)])
list_plot([m[x[0],x[1]] for x in H4],plotjoined=True)
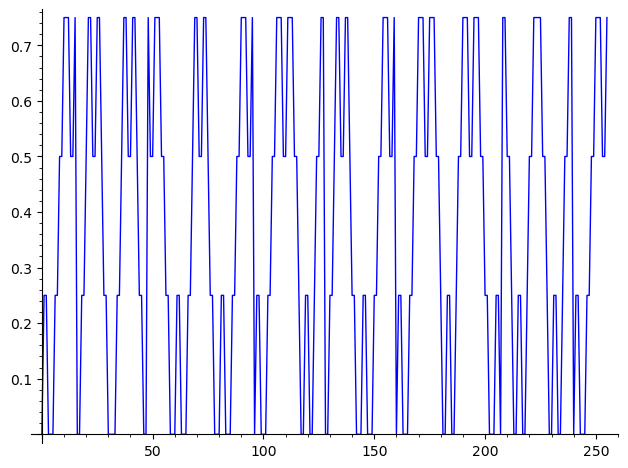
Kompresja metodą krzywej Hilberta#
Kodujemy obraz za pomocą współrzędnych generowanych przez pewną iterację krzywej Hilberta. Następnie wartości pikseli są zamieniane na liczby rzeczywiste. W kolejnym kroku stosujemy dyskretną transformatę Fouriera do ciągu ((a_n)_n) i otrzymujemy rozkład spektralny. Kompresja (stratna) polega na usunięciu z zapisu spektralnego pewnych częstości o najmniejszych amplitudach.
Odwrócona dyskretna transformata Fouriera odtwarza nam (niedoskonałą) kopię oryginalnego obrazu.
A=[RR(m[x[0],x[1]]) for x in H4]
J = list(range(len(A)))
s = IndexedSequence(A,J)
t=s.fft();
list_plot([abs(x) for x in t.list()])
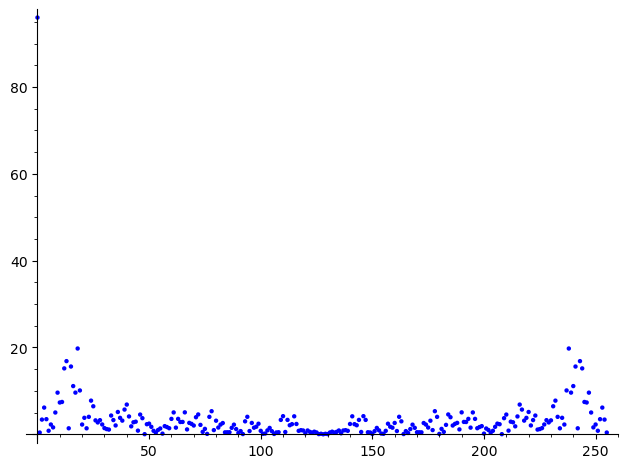
tt=t.list()
tts=[]
for el in tt:
if abs(el)>1:
tts.append(el)
else:
tts.append(0)
A2=tts
J2 = list(range(len(A2)))
s2 = IndexedSequence(A2,J2)
t2=s2.ifft();
mrec=matrix(RealField(),16,16,[0]*256)
for el in zip(H4,[abs(x) for x in t2.list()]):
a,b=el[0]
mrec[a,b]=el[1]
matrix_plot(mrec)
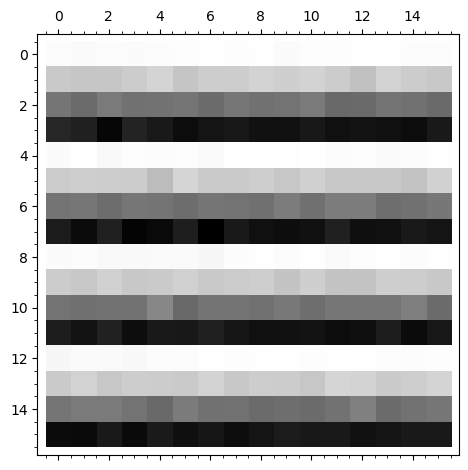
Stratna kompresja syntetycznego obrazu paskowego pokazuje dość duży udział szumów w rekonstrukcji obrazu. W podanym przykładzie uzyskaliśmy tylko stopień kompresji równy 30 procent. Jak zobaczymy poniżej na przykładzie obrazu kota, rekonstrukcja rzeczywistych obrazów pozwala uzyskać dużo wyższy poziom kompresji przy zachowaniu zadowalającej jakości.
list(map(lambda x: abs(x)<0.001,tts)).count(True)/len(tts)
0.30078125
import numpy as np
import matplotlib.pyplot as py
arr=py.imread('figs/cat2.png')
#konwersja na odcienie szarości
def rgb2gray(rgb):
return (np.dot(rgb[...,:3], [-1,-1,0]))/2
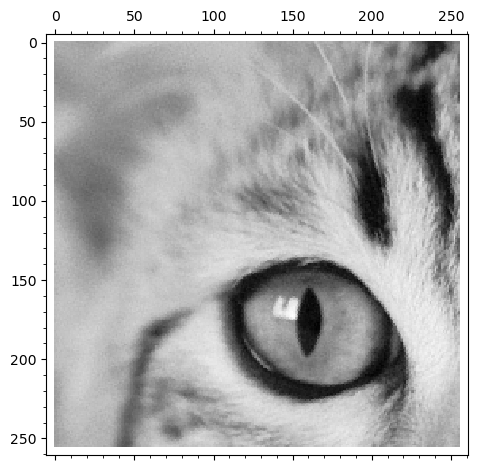
matrix_plot(rgb2gray(arr),frame=False)

kk=rgb2gray(arr)
oko=(kk.transpose())[256:512].transpose()[256:512]
matrix_plot(oko)
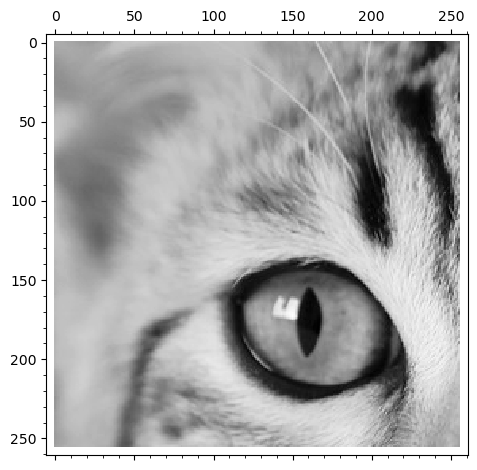
m=oko
H8=HVertices(8)
A=[RR(m[x[0],x[1]]) for x in H8]
J = list(range(len(A)))
s = IndexedSequence(A,J)
t=s.fft();
list_plot([abs(x) for x in t.list()])
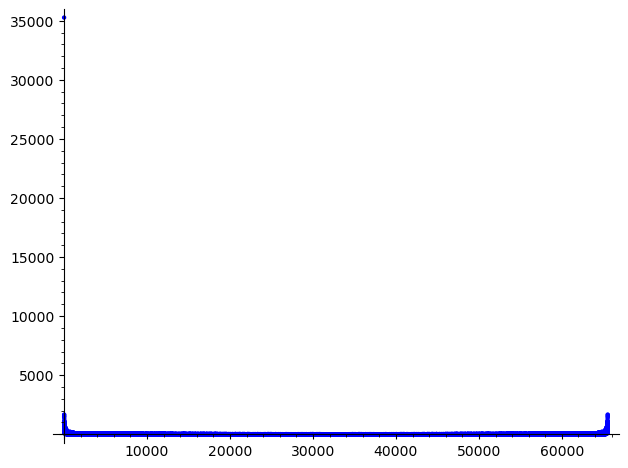
AA=[abs(x) for x in t.list()]
[min(AA),max(AA)]
[0.0423108842316575, 35270.2990471341]
Wartości transformaty o największym module mają dominujący wpływ na obraz. Wyrzucenie wartości o najmniejszych normach skutkuje pogorszeniem jakości, ale odcinając na odpowiednio wysokim poziomie możemy uzyskać zadowolającą jakość.
list_plot(sorted(AA))
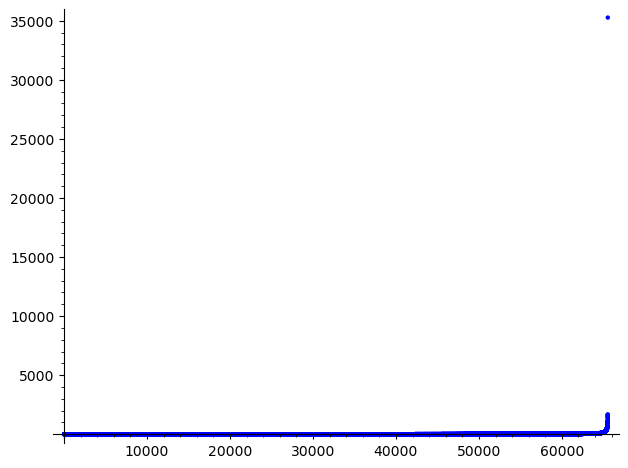
# ostatni element o normie mniejszej niż 10
AAs=sorted(AA)
AAs[46274]
9.99937812254643
[min(A),max(A)]
[-0.986274510622025, -0.0333333341404796]
tt=t.list()
tts=[]
for el in tt:
if abs(el)>10:
tts.append(el)
else:
tts.append(0)
A2=tts
J2 = list(range(len(A2)))
s2 = IndexedSequence(A2,J2)
t2=s2.ifft();
mrec=matrix(RealField(),256,256,[0]*(256**2))
for el in zip(H8,[1-abs(x) for x in t2.list()]):
a,b=el[0]
mrec[a,b]=el[1]
matrix_plot(mrec)
#współczynnik kompresji uzyskanej w wyniku usunięcia z transformaty wszystkich wartości o normie większej od 30
list(map(lambda x: abs(x)<10,tts)).count(True)/len(tts)
0.7061004638671875
